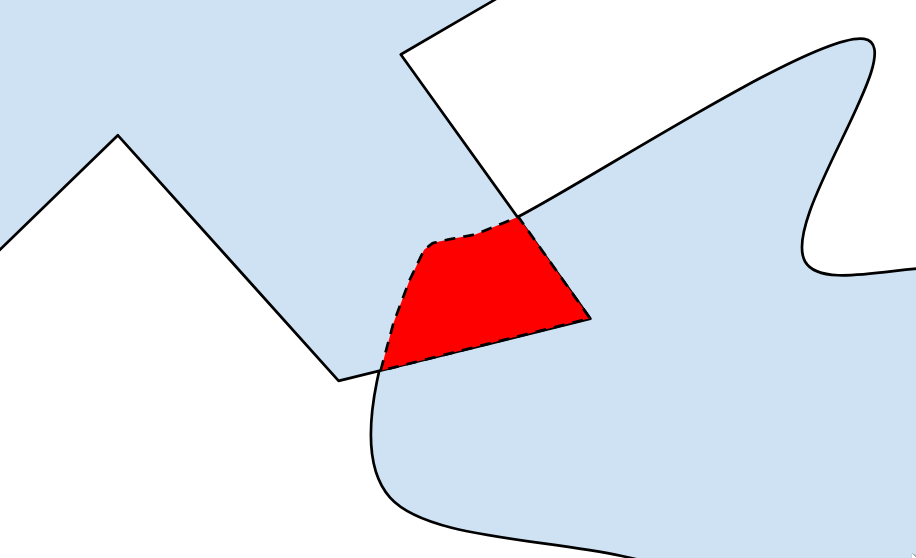
The GJK algorithm is a weird way to do a simple thing.
We have shape A and shape B, and we'd like to determine if they overlap.

A shape is a set of infinitely many points. If there exists any point that's a member of both sets, then the shapes overlap.
Alternatively, if there exists point a in set A and a point b in set B such that:
a - b = 0
Then an intersection exists. Note that the 0 here represents a point itself: the origin.
To see what this means intuitively, we can take a shift in perspective. Instead of dealing with specific points, let's try subtracting every point within one shape from every point within another, and plotting where they all end up:

We've ended up with a new set that represents the "difference" between A and B. Since it contains the origin, we know that there must be at least one pair of points whose difference is 0.
That's exactly what the GJK algorithm takes advantage of. Instead of directly checking if the sets have an intersection, we subtract them and see if the new set contains the origin.
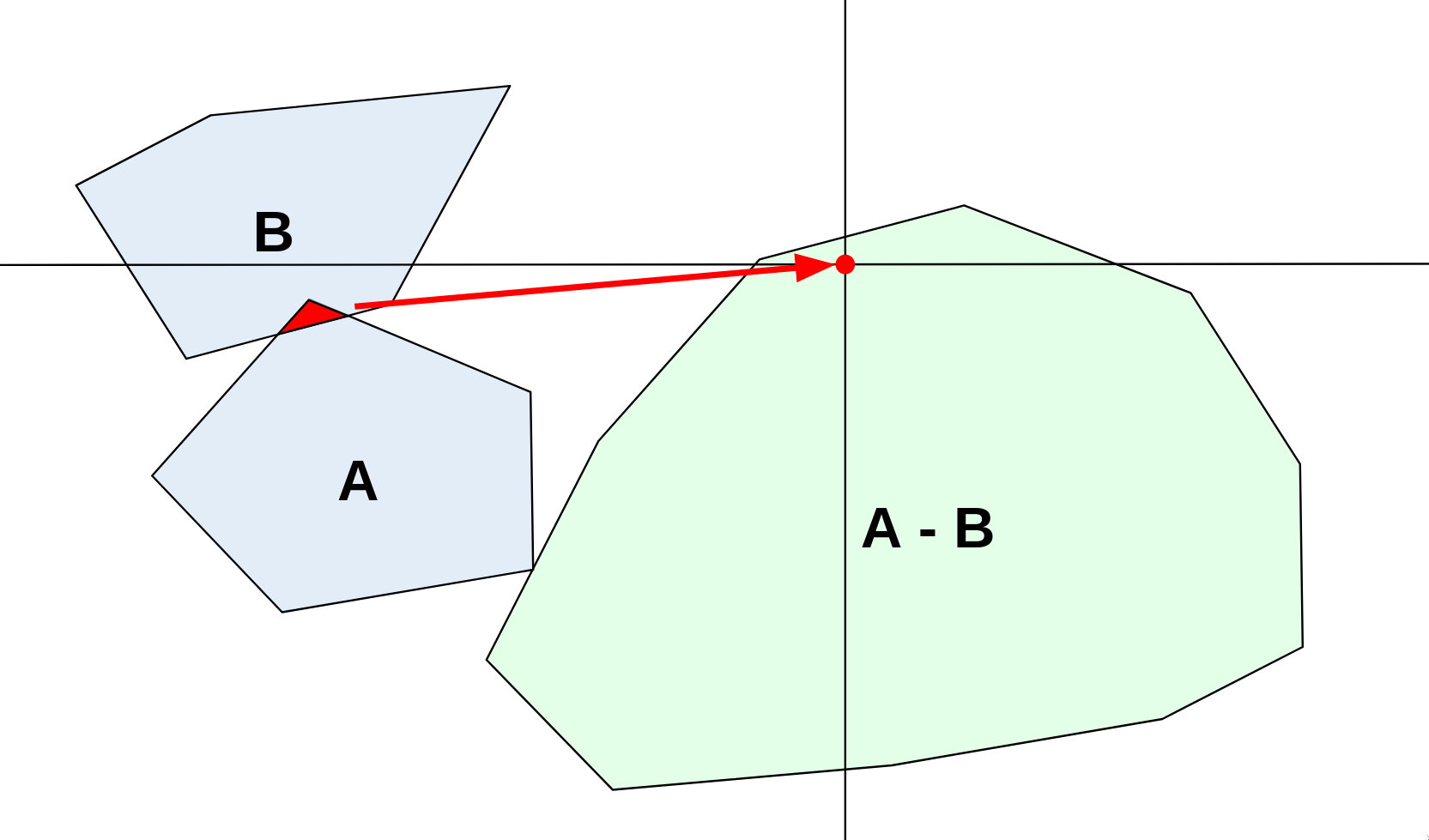
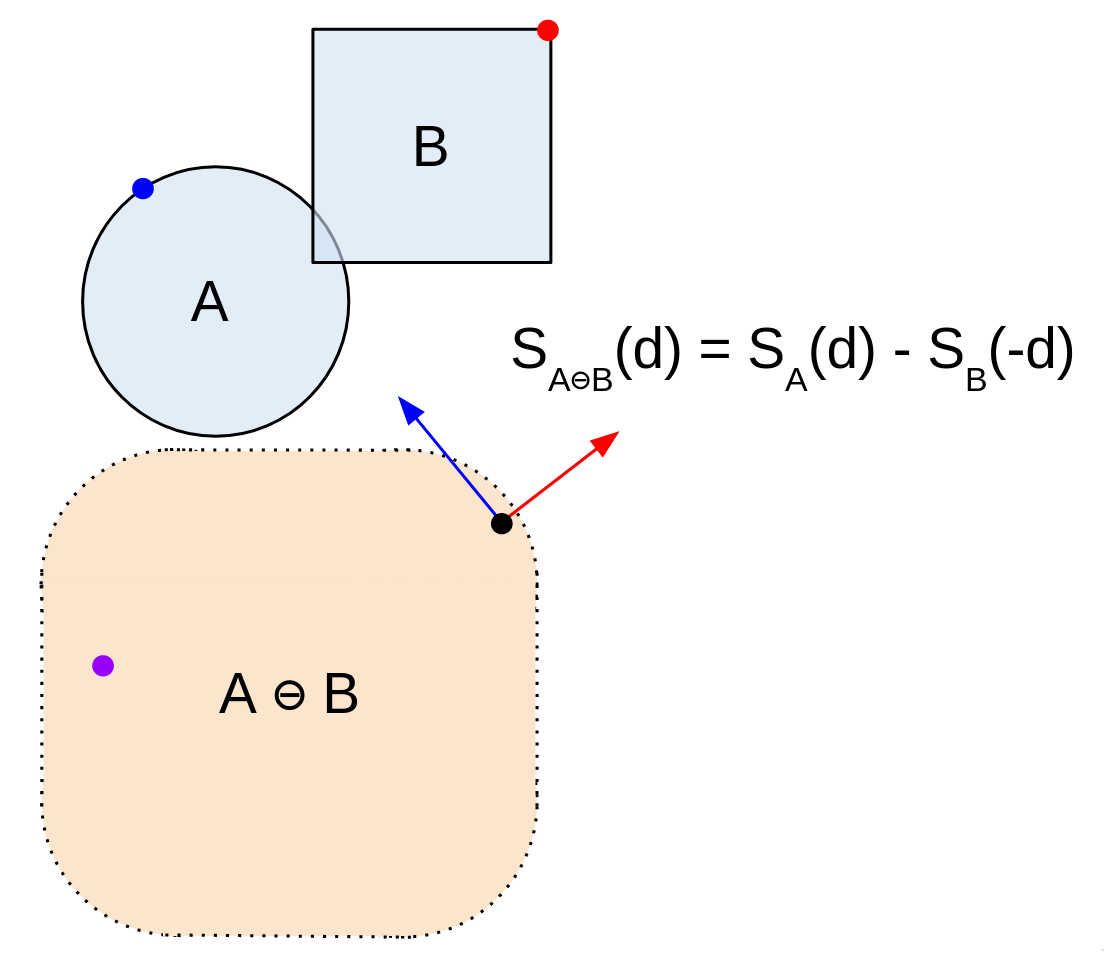
Combining sets like this is known as taking the Minkowski difference. You may see this denoted '⊖' to separate it from the normal notion of a difference.
More formally, it's defined as:
A ⊖ B = {a - b | a ∊ A, b ∊ B}
At first, it doesn't seem like we've made any progress, only rephrased the problem. How are we supposed to subtract infinitely many points? Well, let's find the bare minimum that we need to know about the set A ⊖ B to see if it contains the origin.
In 2 dimensions, if a convex set contains the origin, it means we're able to draw a triangle between 3 points on the boundary, which contains the origin. This makes the problem even easier. If we know that A ⊖ B is convex, we only need to deal with the boundary.
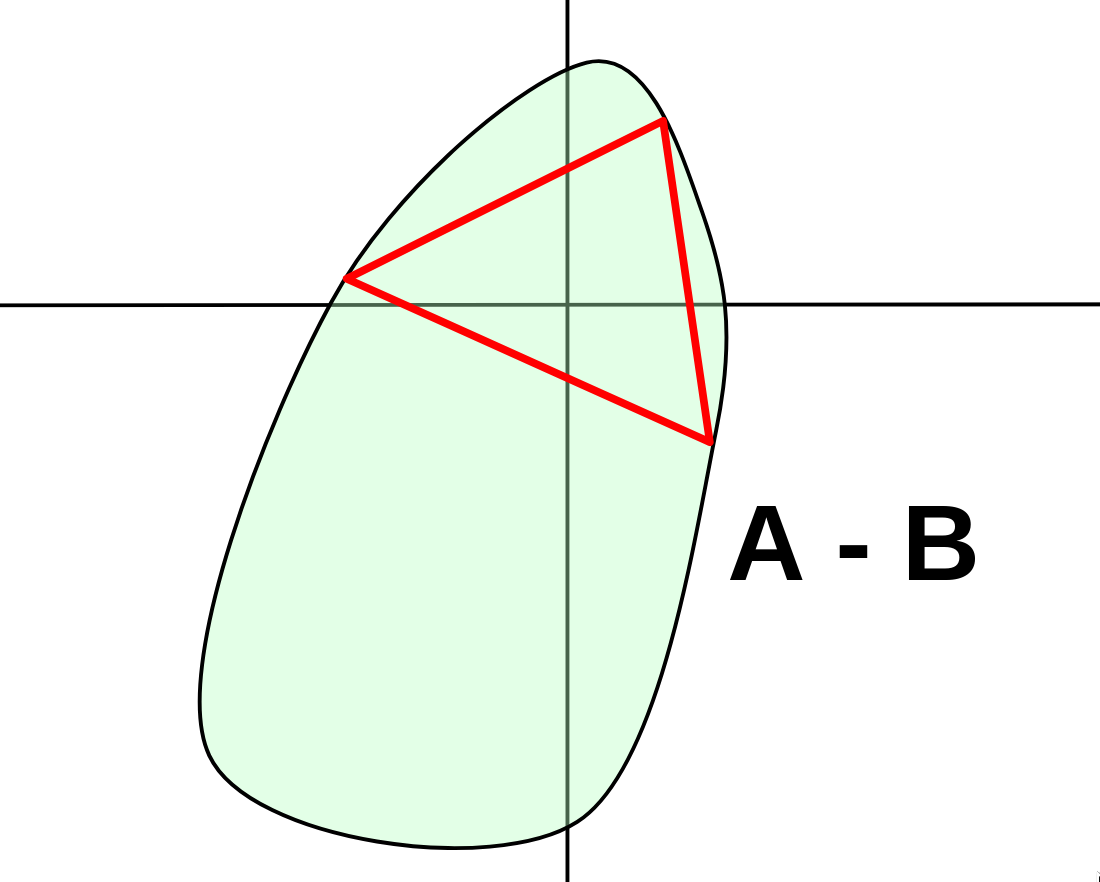
Luckily, it's easy to ensure A ⊖ B will be convex.
The Minkowski difference of any two convex sets is also convex. So, we just need to break down A and B into convex components, which we can work with individually. On a computer, most shapes are already constructed out of convex components, so this process is often extremely easy.
By the way, even though I'm explaining in 2D, our problem is fundamentally the same in any dimension. Here, we're looking for a bounding triangle on A ⊖ B. But, more generally, we're looking for a "simplex" in our dimension. An n-dimensional simplex is just the simplest polytope that can enclose an n-dimensional region. For example, a 3D simplex is a tetrahedron, as it has the fewest vertices needed to bound a volume.
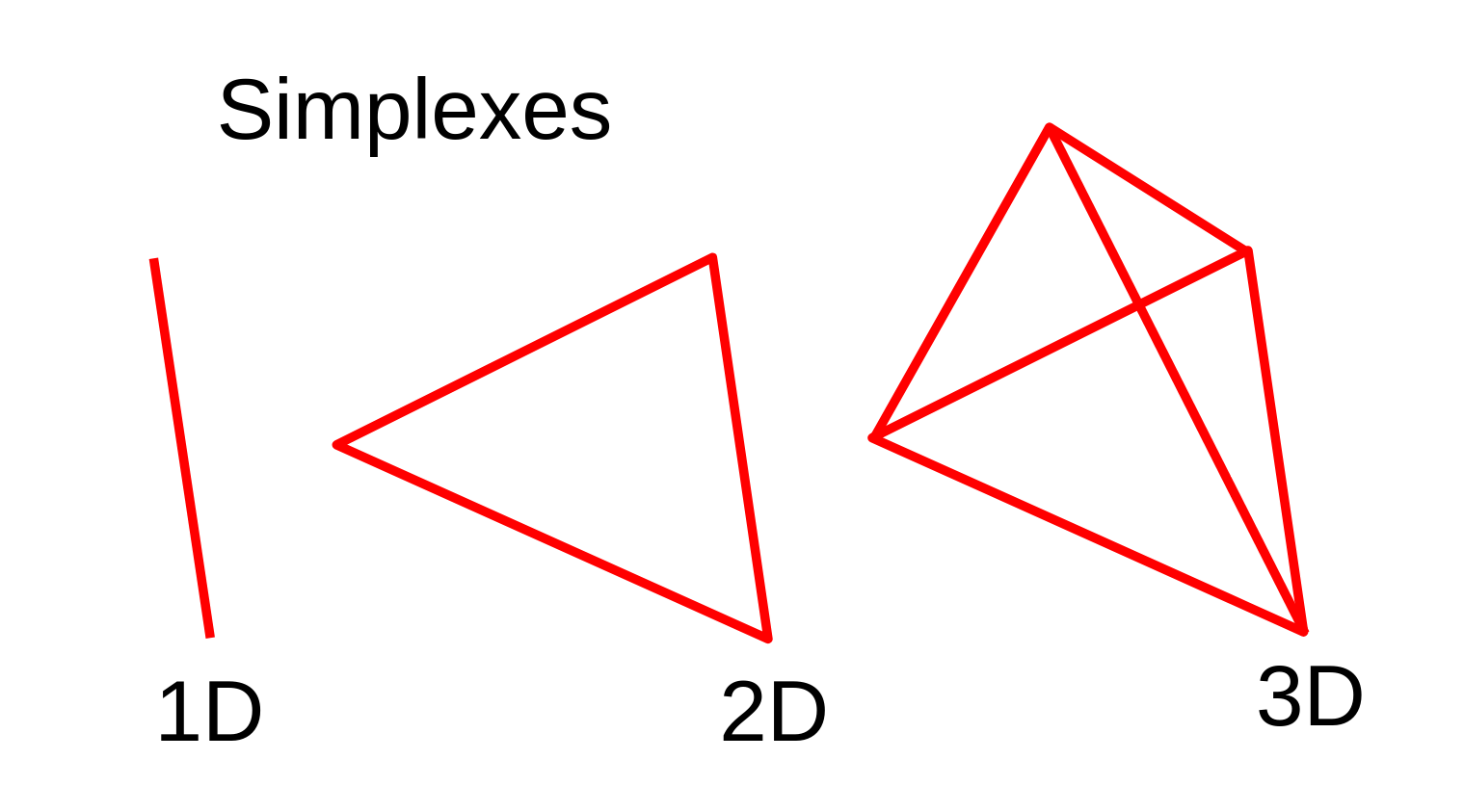
With these tools, let's restate the problem.
So, from now on, whenever I say "shape", I'm speaking only about the boundary of a given set. We've thrown away all the area, as it's no longer relevant to the problem.

Things would be much easier if we had some system to identify points on our shape. The support function (denoted S here) does just that. It takes in a vector, and outputs the furthest point on the shape in that direction. On a convex shape, every boundary point is identifiable using the support function of some direction.
In other words, if we rotate a vector d 360 degrees around the origin, S(d) will hit every point. So, finding N points on a shape corresponds to finding N directions.
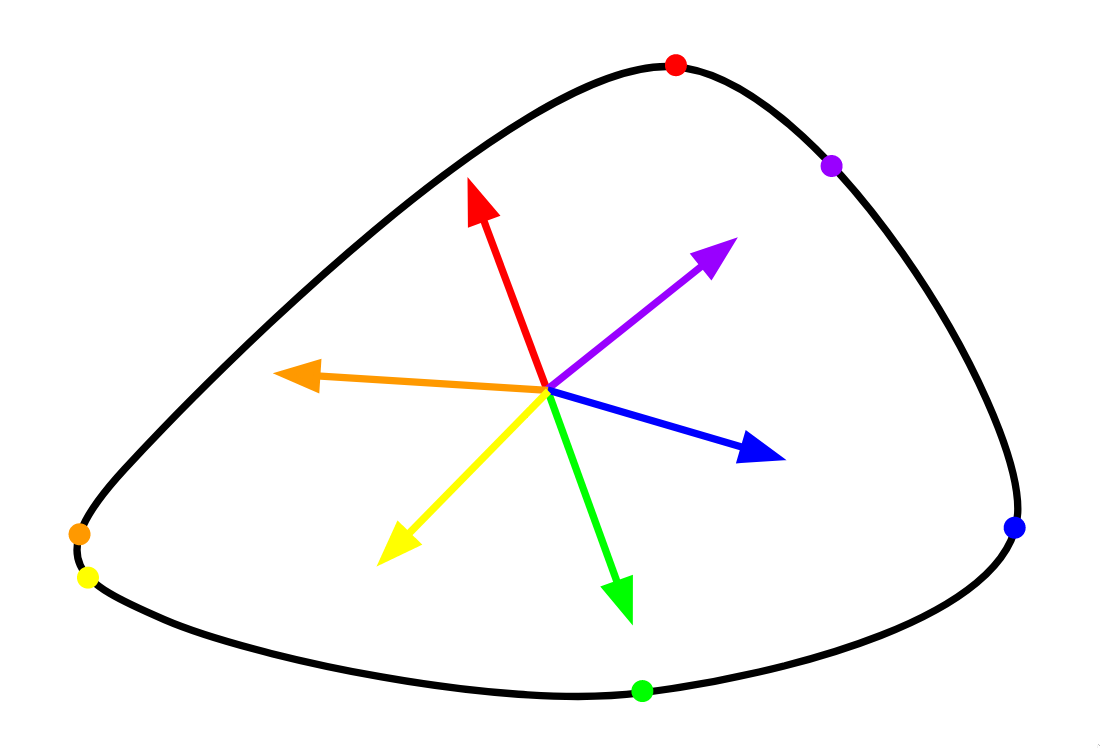
The support function is easy to formally define. It's just the point that has the highest dot product of d.

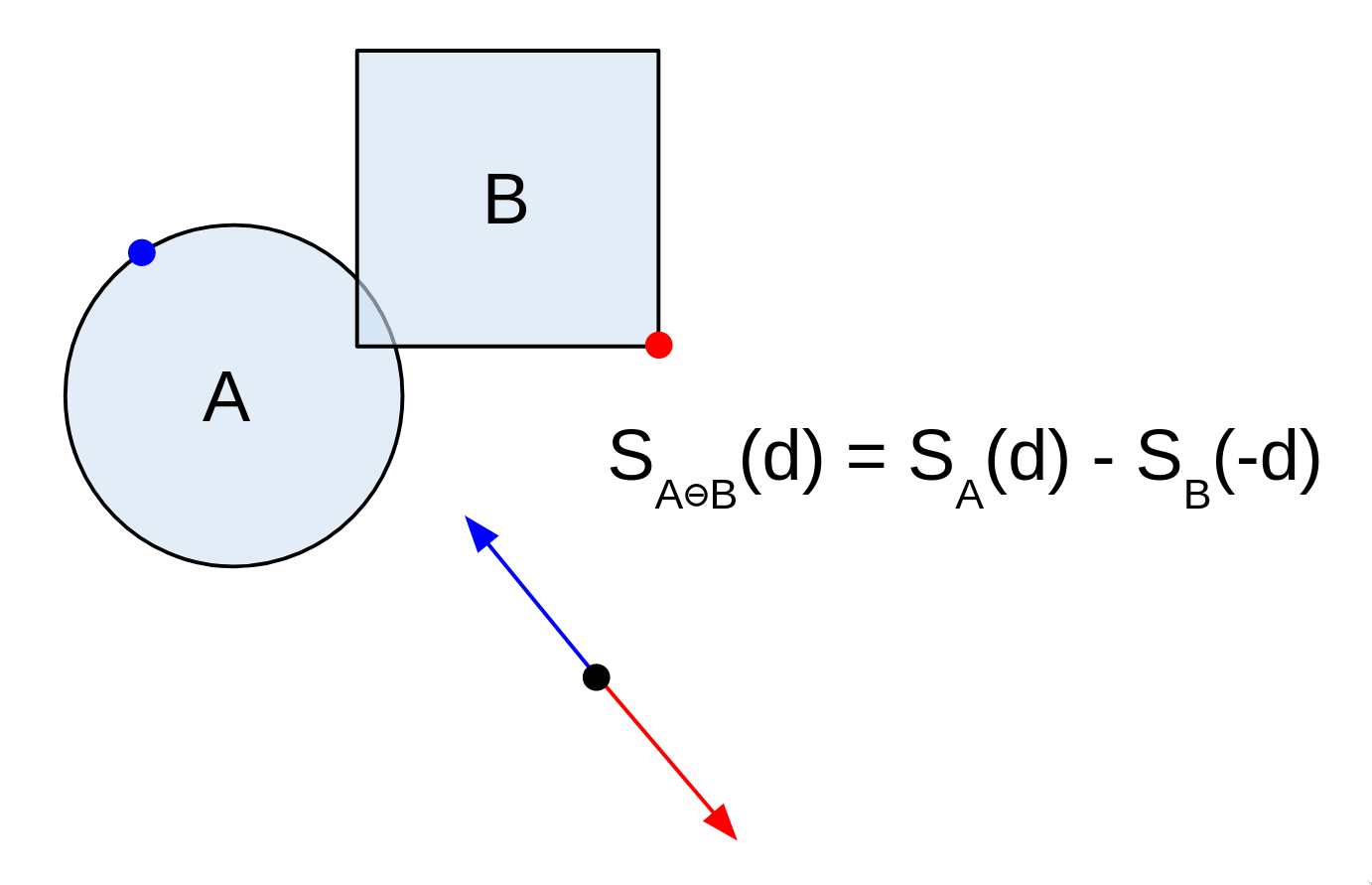
Remember how I previously said we'd need to find 3 points on A, and 3 points on B? Well, we really only need to find 3 points in total. That's because of the following useful property of the Minkowski difference:
The support of direction d in A ⊖ B = the support of d in A minus the support of -d in B.
Basically, if we sweep across the borders of A and B in opposite directions by rotating d, we'll hit every boundary point on A ⊖ B. This massively narrows down how many possible points we need to search, as our points on A and B will always be dependent on each other. I know the diagrams are getting a bit confusing now, so bear with me.

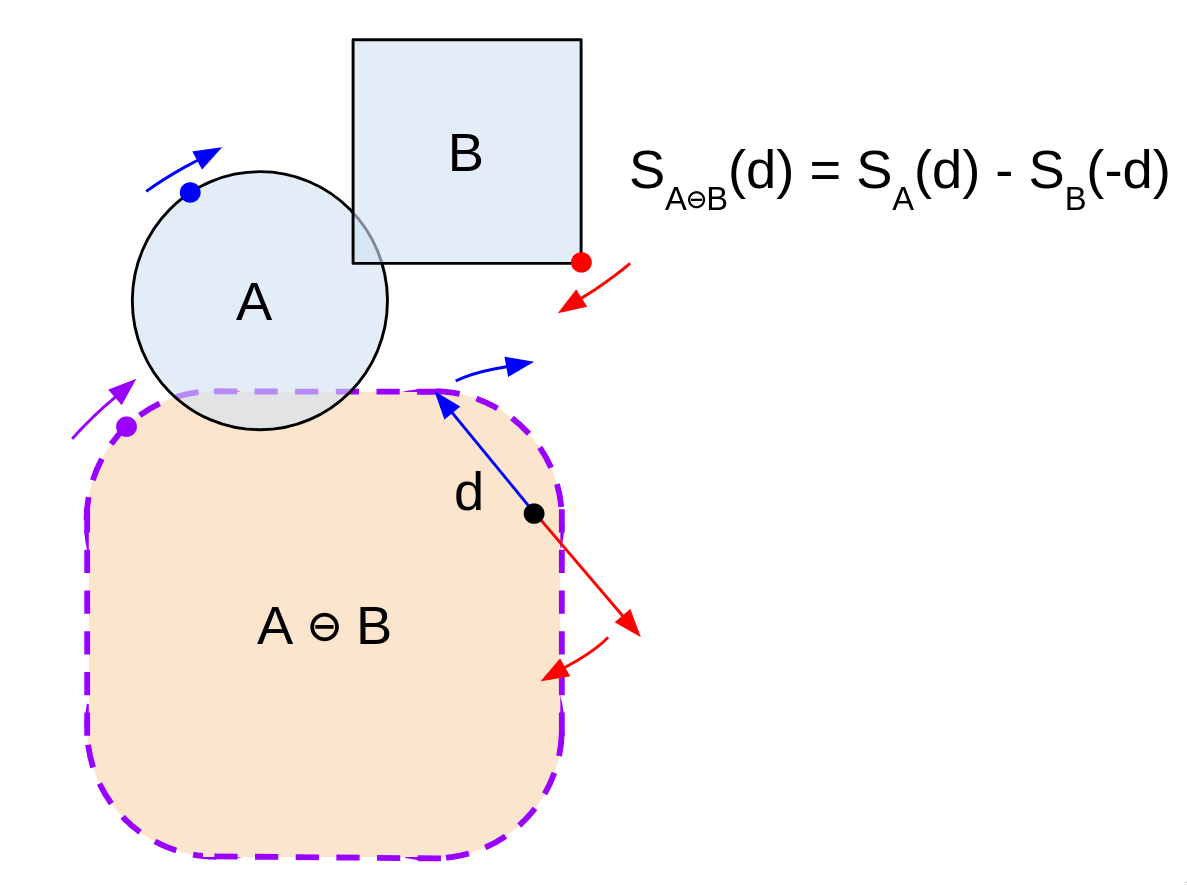
Put differently, most combinations of points on A and B don't matter, as they won't land us on the border of A ⊖ B. We only need to consider the case where they're in opposite directions. (There's some easy intuition for why this is the case: I'll leave that as an exercise)
Alright, the stage has been set for GJK. The goal of the GJK algorithm is to find a simplex on A ⊖ B that contains the origin (or show that none exists), while doing as few operations as possible.
Let's appreciate how incredible such an algorithm would be: given any convex shape, as long as it has some defined notion of support points, we can detect collisions. That's unbelievably powerful.
Here's how it works:
1) First, find a point on A ⊖ B using a random direction d, which we'll call p. This is just S(d) - S(-d). It's the first point on our simplex.
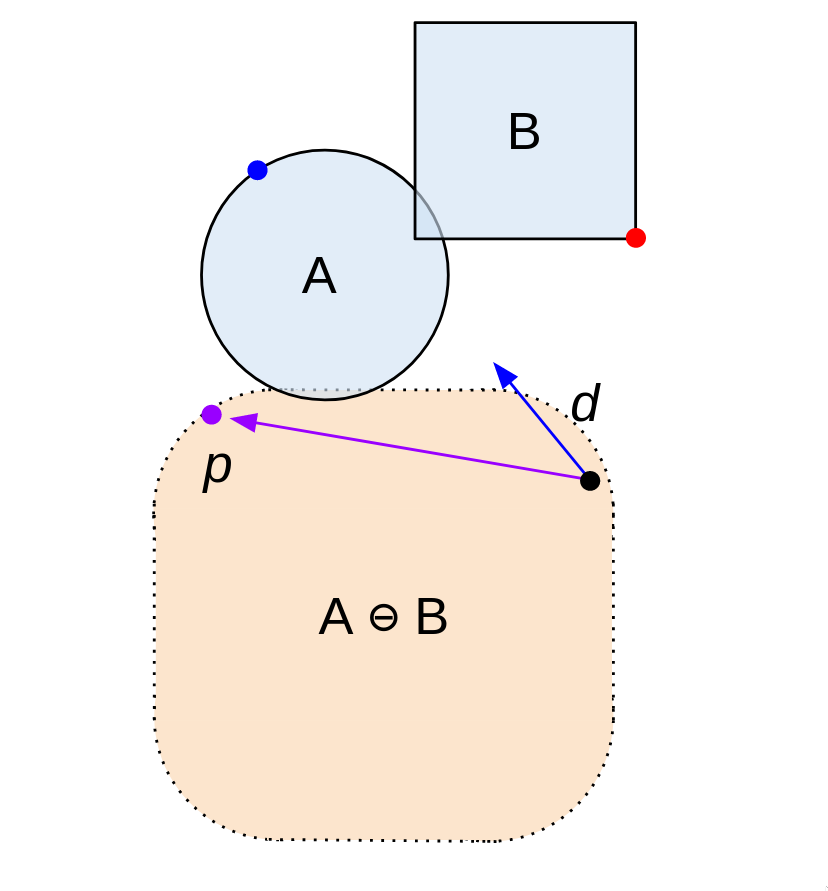
2) Then, let's take the dot product of d and p. If it's positive, we keep going on with the algorithm. If it's negative, that means d and p point in opposite directions. In that case, we terminate the algorithm, as there's no way for B and A to overlap.
But why?
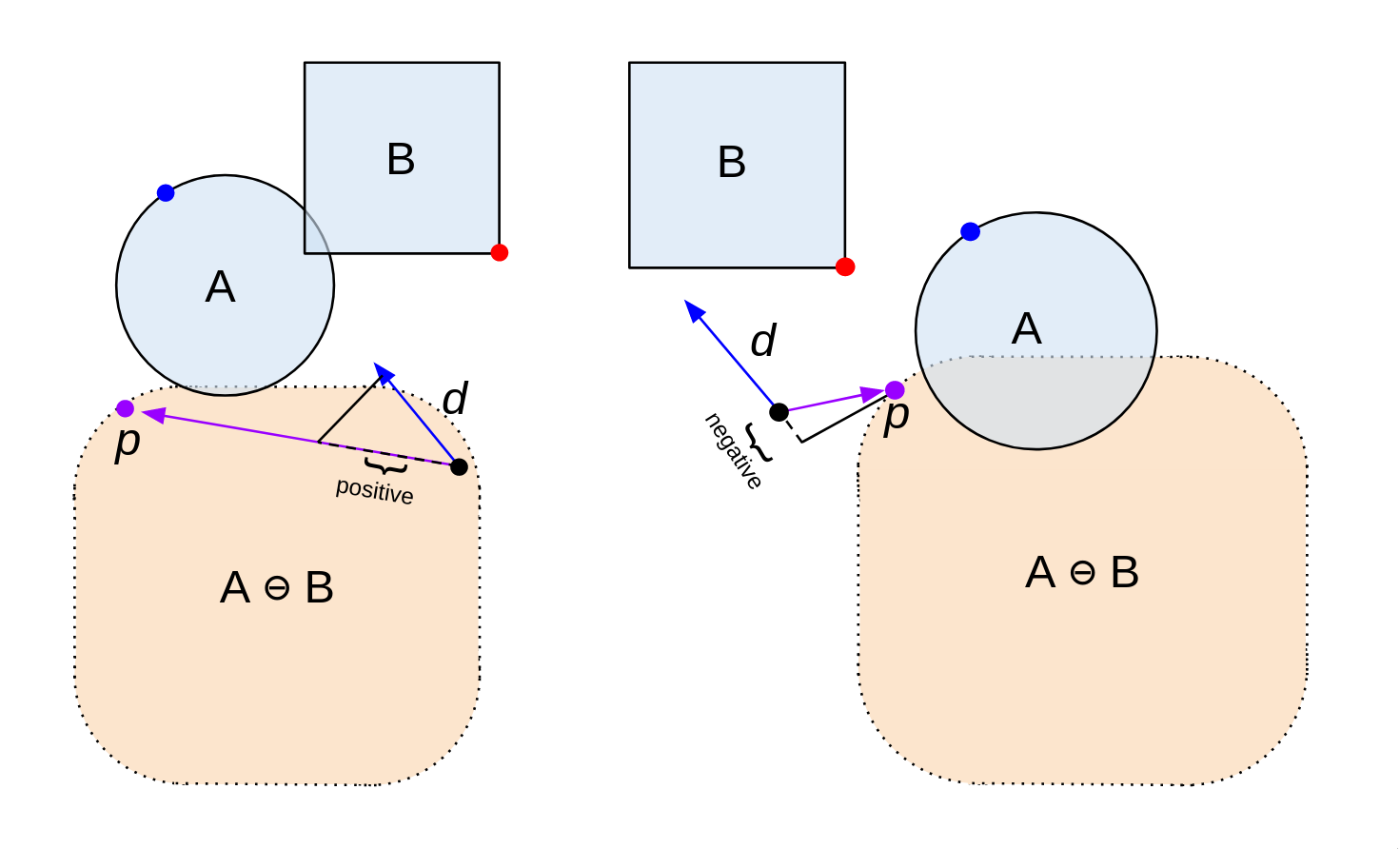
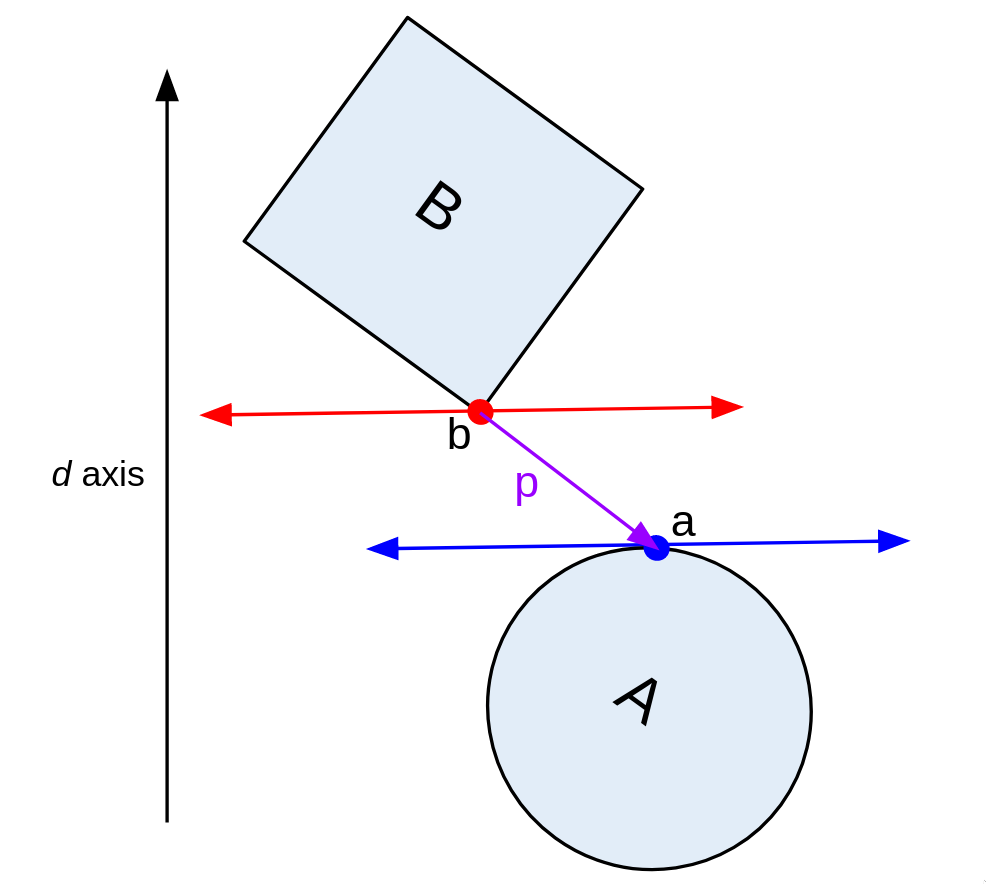
It's more clear when we rotate our view to be in line with d. Point a is S(d), and point b is S(-d). Now, point a is the "top" of shape A, and point b is the "bottom" of B. Remember that p = a - b. So, if we project p onto d by taking the dot product, and it's negative, a gap exists between A and B.
3) Ok, great. We've got one point of our simplex. Now, we need another. From our point p, let's shoot in the direction of the origin. Take the support of that vector -d, and run our check from step 2 on it.
If you think about it, we're just finding the point most in the direction of the origin from p. If our shape encloses the origin, then our new point will have to be on the opposite side of it.
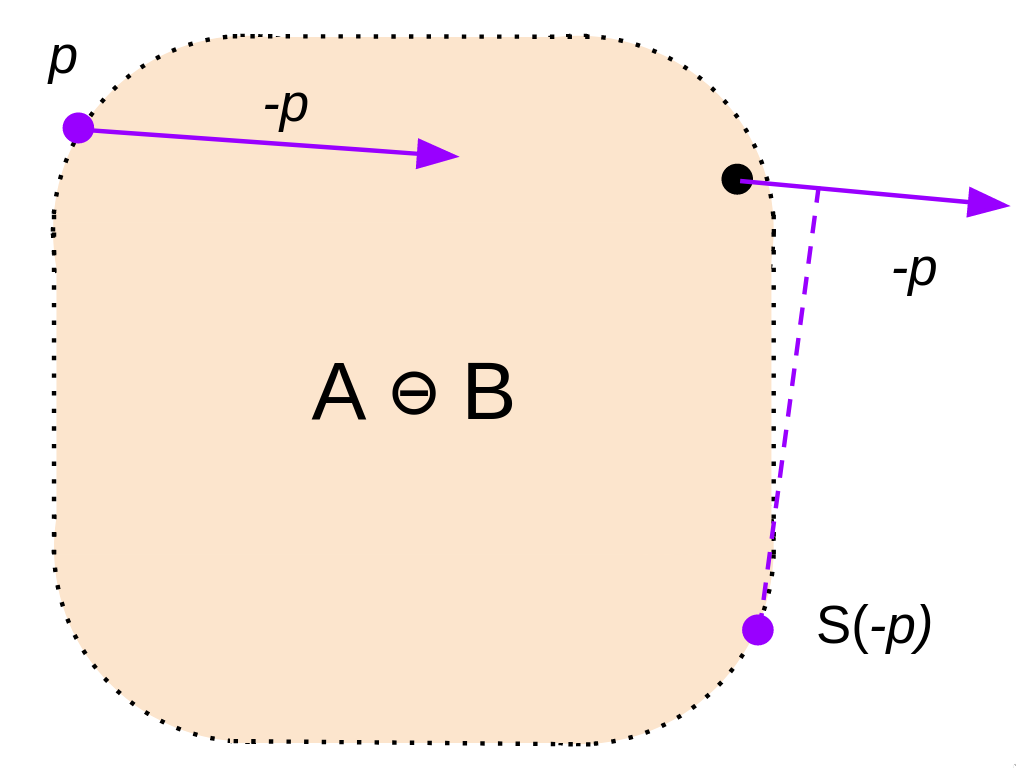
Remember how we just performed the check from step 2? Well, there's another way to think about it. We're just checking to see if we've crossed the origin. If the origin is within our shape, we'll have to cross it when we take support points in opposite directions.
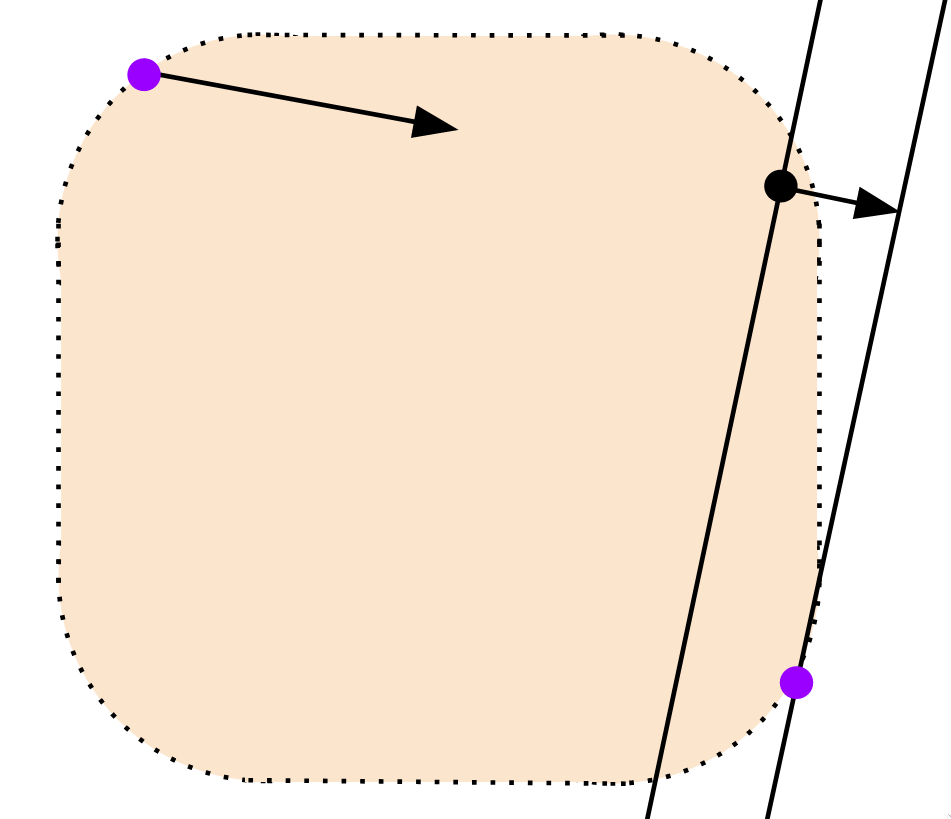
4) Now, we're ready to complete the simplex. Let's take the vector perpendicular to our first 2 points in the direction of the origin. The support of that vector is the 3rd point of our simplex.
I mean, think about it. We've effectively divided the space in half with our first line. We know the origin can't be anywhere on one side of our line, so we continue our search in the opposite direction. That's the efficiency of GJK: we'll keep dividing the space in half, until we find the point.
Oh, and as usual, we can run our check from step 2 to see if we've proven that the shapes do not overlap.
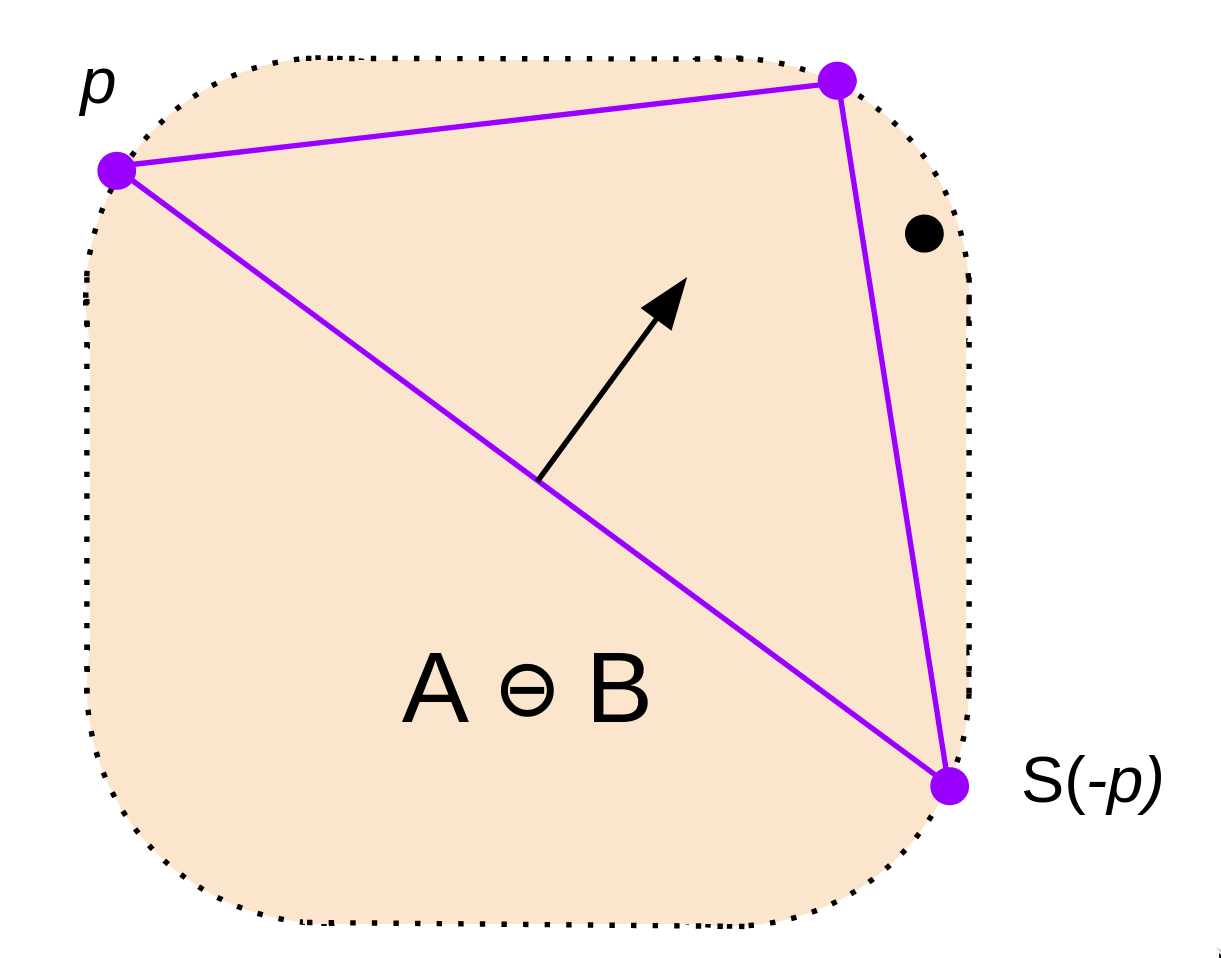
5) Now, let's see if our simplex contains the origin. If it does, we return true. Otherwise, we continue on.
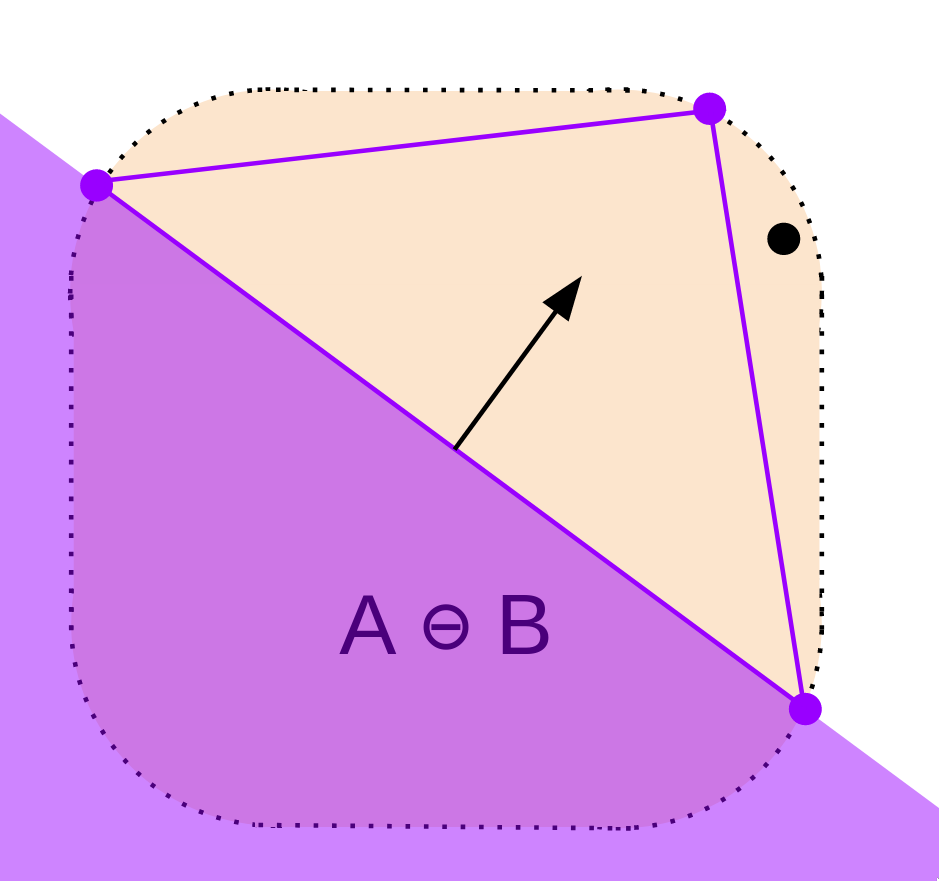
To find if the origin is within our triangle, first, let's break down the area surrounding it into the three infinite regions depicted below.
The overlapping red, green, and blue regions each divide the space in half: an inside region, and an outside region.
We've already eliminated the possibility of the origin being in the red region. So, we just have to check whether it's outside either of the remaining 2 lines.
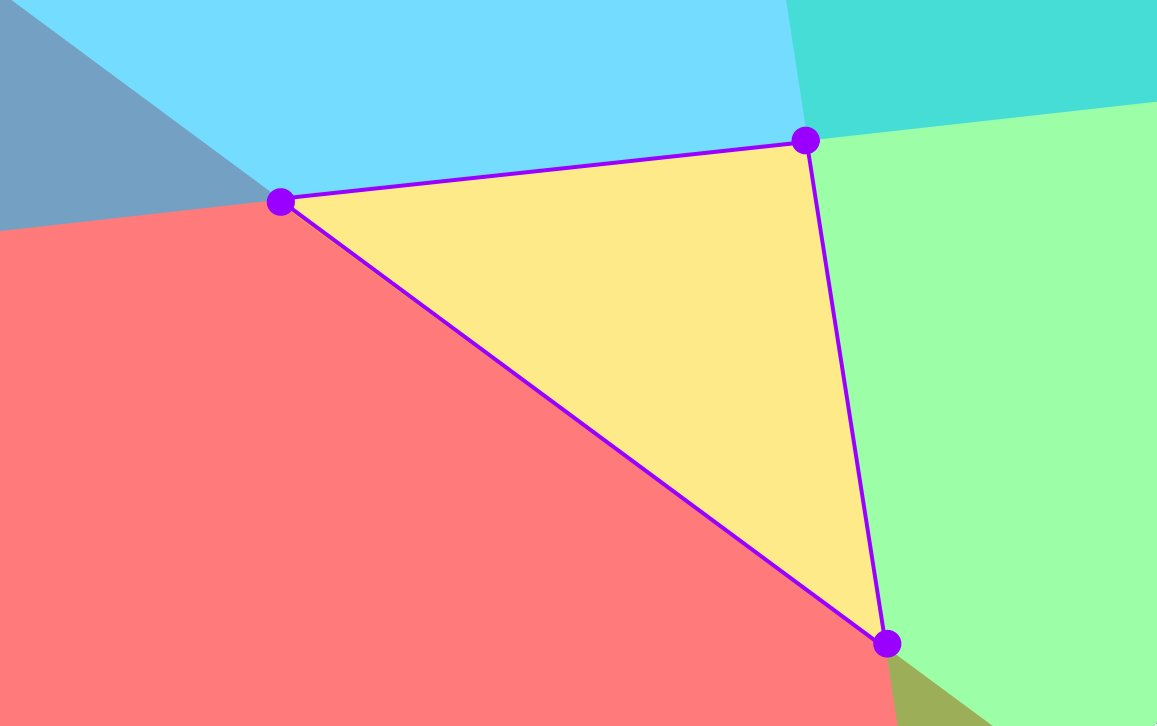
Luckily, we already know how to do this. Just take the dot product perpendicular to a given line to see if the origin is beyond it. If so, we know it must be in the white region.
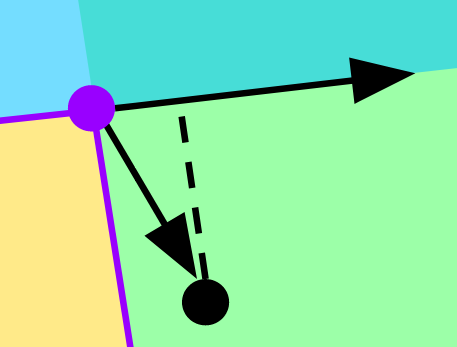
6) Now, it's time to iterate. We repeat from step 4, this time from the line on our simplex closest to the origin. We update our simplex using this new support point, and check if the new simplex contains the origin, as we did in step 5. This time, it does! Our algorithm returns true. If it doesn't, we keep doing this iterative process until it does, or one of our checks fails.

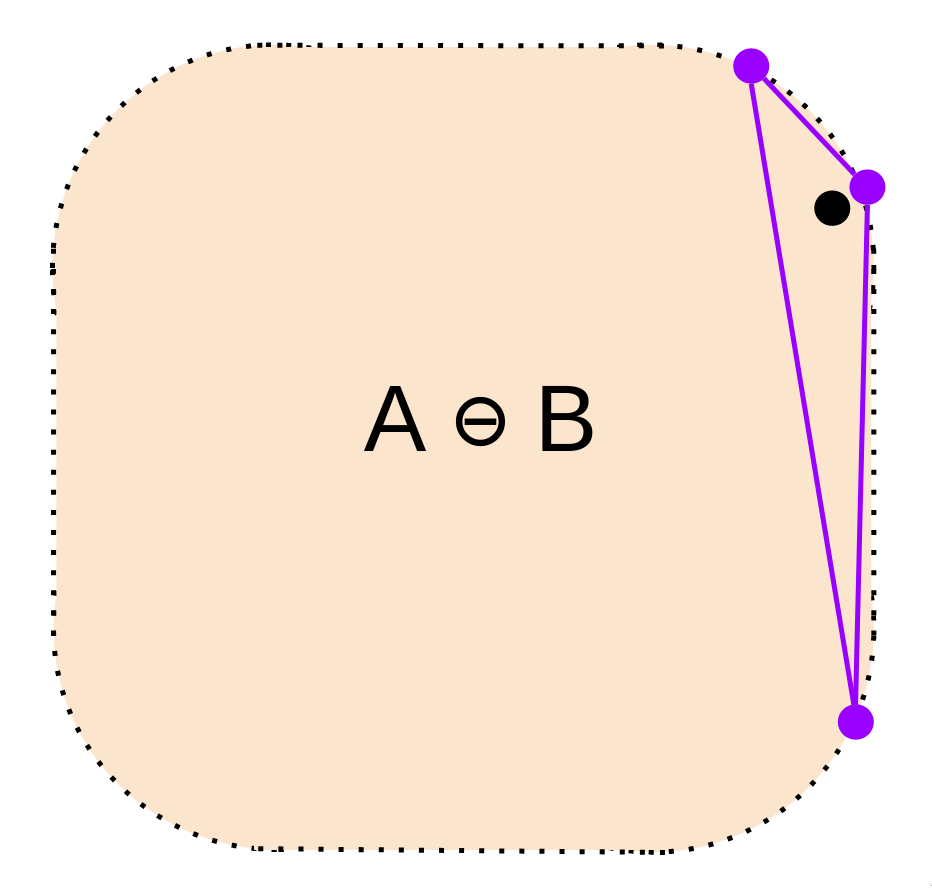
And, that's it. That's the essence of the GJK algorithm.
I've glossed over a few implementation details, but you now have all the intuition you need to develop an in-depth understanding.
Personally, I find this algorithm pretty because it's such a tidy example of what makes mathematics so powerful. Through a bunch of subtle shifts in perspective, a complicated problem becomes obvious.
There's probably a few things incorrect with what I said. So, take it with the appropriate amount of salt for a high school sophomore's explanation of anything math related.