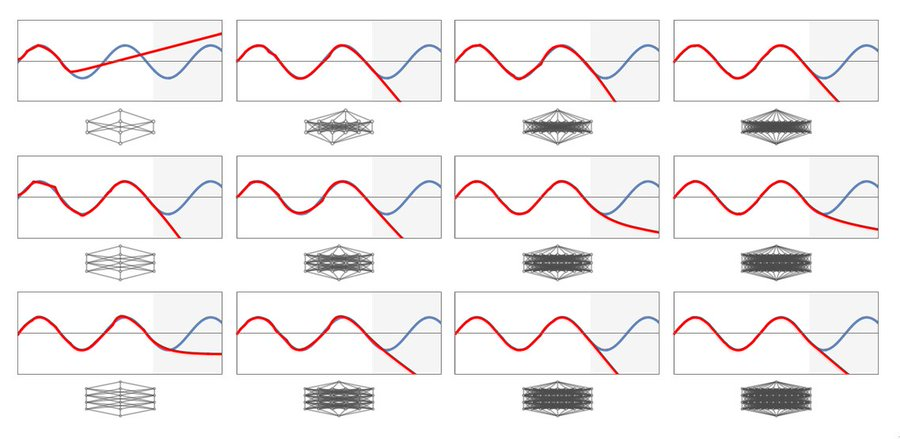
Why can't MLPs ever learn sine waves? So, for context, Stephen Wolfram wrote "Can AI Solve Science?" a few months ago arguing that neural networks can't generalize beyond their own training due to the constraints of architecture. A particularly interesting example was showing that an MLP fails to generalize simple periodic functions beyond the training range, even with several layers:

Although it's disappointing, it makes sense intuitively:
An MLP with an aperiodic activation function just doesn't have any way to apply a periodic pattern across the entire range of (-∞, ∞). While the range can be stretched, squished, and rotated as it flows through the hidden layers, each portion has to be treated individually.
What can we do about this? Well naturally, if we give a network access to a sine activation function, it's trivially capable.
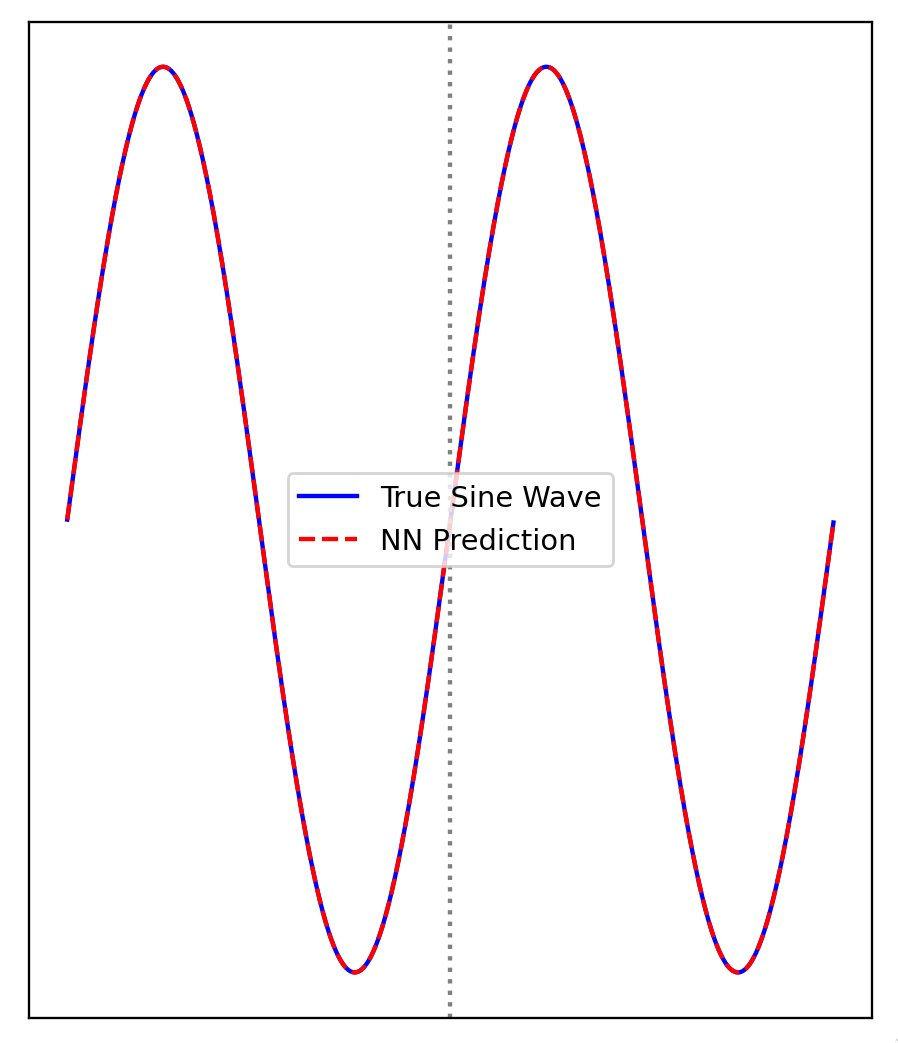
This is cheating, of course -- we've given it the solution. Will we always have to change the architecture to fit the problem as we did here? To answer that question, we'll need a more general explanation of what's going on here.
To understand something, a neural network, just like a human, has to create an abstract representation of it that compresses away all the noise, and captures what really matters. Often, this comes in the form of recognizing different symmetries.
An MLP with a typical aperiodic activation function has to treat each patch of linear input-space separately -- it can't represent this positional invariance. We need the neural network to have, in its "internal vocabulary" of concepts, this notion of periodicity.
(The paper "Neural Networks Fail to Learn Periodic Functions and How to Fix It" goes in depth about the family of activation functions which are capable of capturing periodicity.)
So, have we found a fatal flaw, fundamentally limiting what a MLP can do? Well, I'd like to provide an alternate way of thinking about it.
There's actually no one correct way to induct a sequence. Any possible continuation is plausible -- after all, we obviously don't know anything about what comes next.
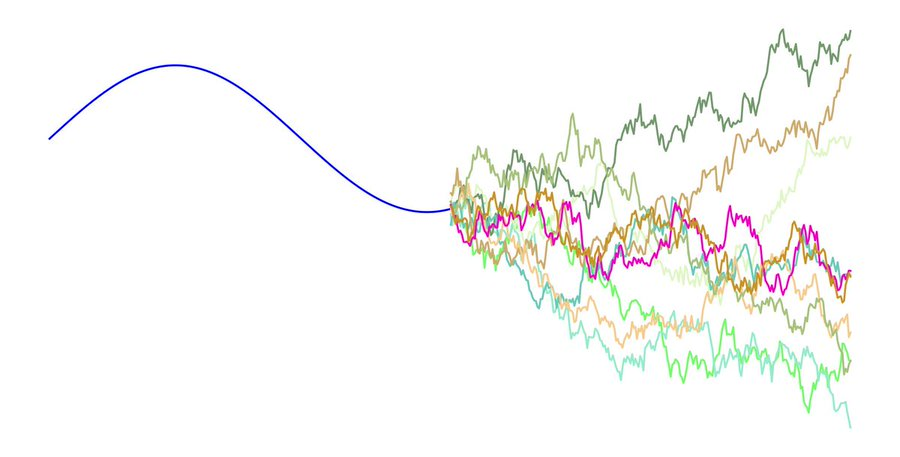
Still, there's one path that makes more sense to us; it's the most simple one. that's the idea behind Occam's Razor.
In other words, we assign a "universal prior" to the infinite possibility space which states more simple things are more likely. This is simply a broad and shockingly accurate generalization of everything humans have learned about the universe.
This can be formalized with Solomonoff Induction:
And, this is the behavior we'd hope to get out of a neural network. In fact, this is why smaller nets often work better -- they model something closer to the minimal program.
But, here's the important part, and the root of our problem:
The "language" is never specified. And, which language we measure complexity with is really important -- different choices result in different notions of what "simple" means. We can call this influence the "inductive bias".
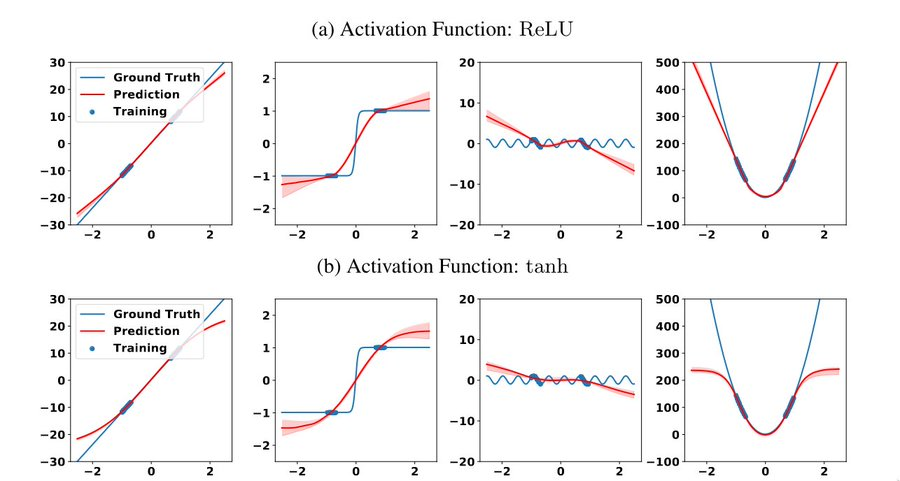
As you can see in the image above, which activation function we use can be thought of as an analogy for the aforementioned inductive bias. We can view the use of different activation functions as causing different definitions of what a simple curve looks like. Each one of these images shows the training data being fit in different ways, but they're all reasonable given their respective inductive priors.
So, to answer the question raised at the start, sine waves are only the optimal fit of the data with respect to the human inductive bias: roughly, natural language and the family of common mathematical functions. Unless the concept of periodic functions is present in the structure of the network, they'll seem infinitely complex to them.
So, the "incorrect" diagrams at the start of this post actually are correct. They're the most likely continuation of the sequence given the setup of the networks.
Instead of a conclusion I'll leave you with a problem statement:
How can we align the inductive bias of machine learning with the inductive bias of reality?
(epistemic status: i am dumb & usually wrong)